AVL树查找、插入和删除在平均和最坏的情况下的时间复杂度均为O(logN),增加和删除元素的操作可能需要借由一次或者多次的树旋转,来实现树结构的重新平衡。
二叉查找树 BST(binary search tree)
也叫二叉排序树 BST (binary sort tree)
- 如果左子树不为空,则左子树上的所有节点均小于根节点的值
- 如果右子树不为空,则右子树上的所有节点的值均大于根节点的值
- 左、右子树也都是二叉查找树
对于一个节点分布相对均衡的二叉查找树来说,如果节点的总数为n,则搜索的时间复杂度就是O(log n)和树的深度是一样的。
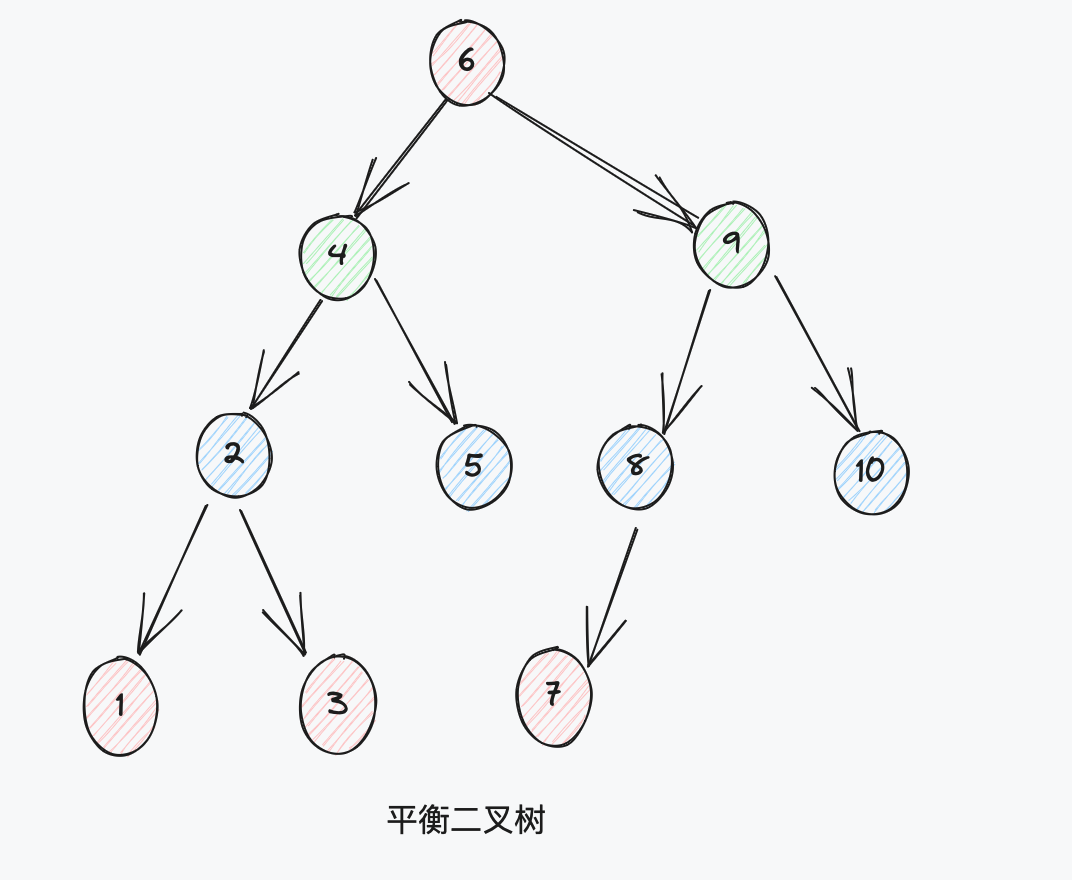
AVL树时间复杂度
| 算法 | 平均 | 最差 |
|---|---|---|
| 空间 | O(n) | O(n) |
| 搜索 | O(log n) | O(log n) |
| 插入 | O(log n) | O(log n) |
| 删除 | O(log n) | O(log n) |
树的平衡
树的平衡是指对于给定数量的节点,保证树的高度尽可能短的过程。如果可以满足树所有叶子结点都在最后两层上,且倒数第二层是满的,则这棵树是平衡的。如果一个平衡树最后一层叶子结点都在最左边的位置上,则这棵树是左平衡的。
平衡因子
某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。一个结点数为n的完全二叉树的高度为 log2(n)
树的旋转
AVL树的基本操作一般涉及运作在同在不平衡的二叉查找树所引用的同样的算法。但是要进行一次或者多次的AVL旋转。以下是四种不平衡的情况以及对应的处理方式。
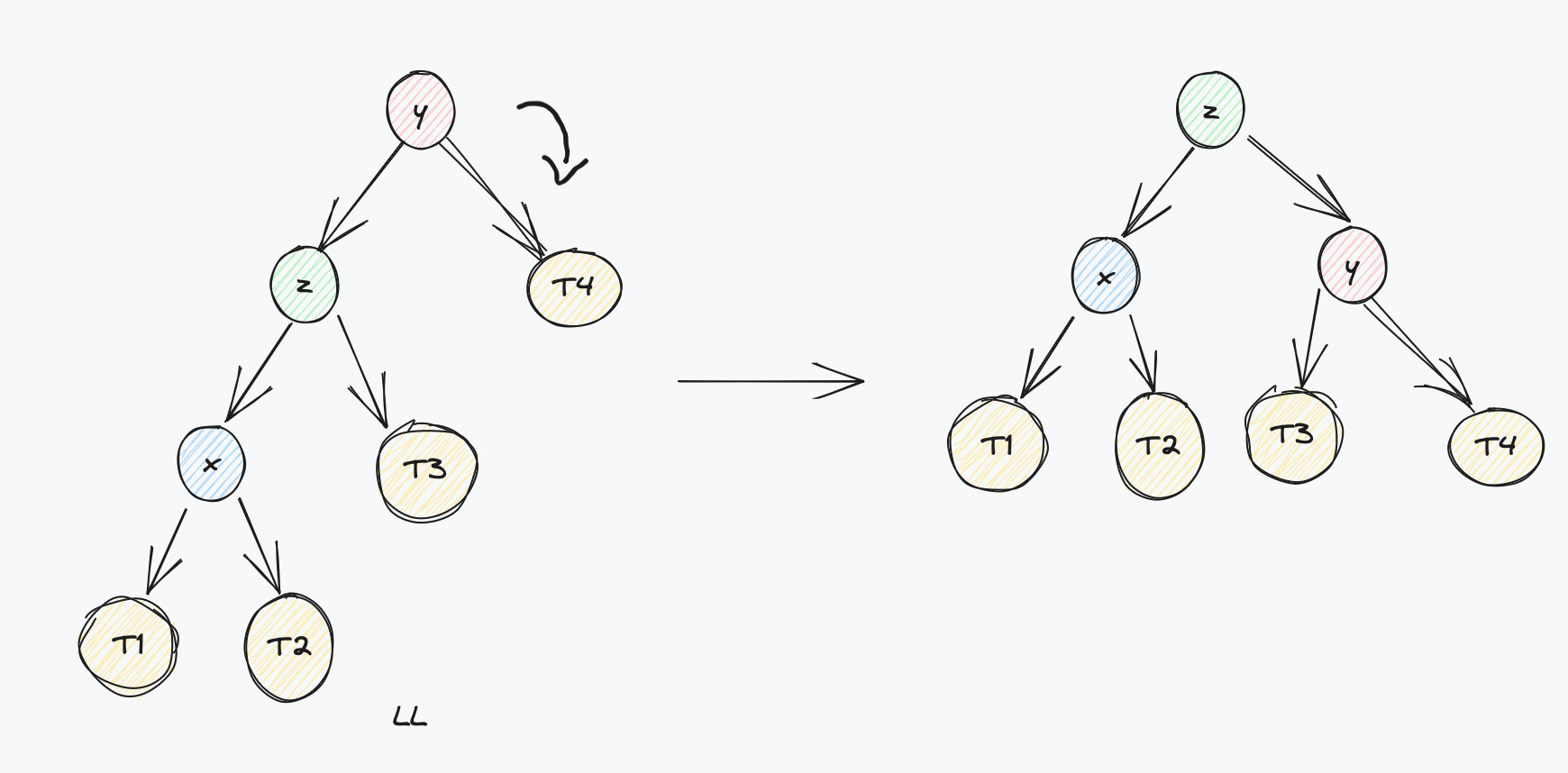
- LL 情况
根节点平衡因子大于1,且其左子树与右子树的高度差大于等于0
处理LL情况,需要将树整体进行右旋转(即对根节点Y进行右旋转,顺时针),效果如下所示:
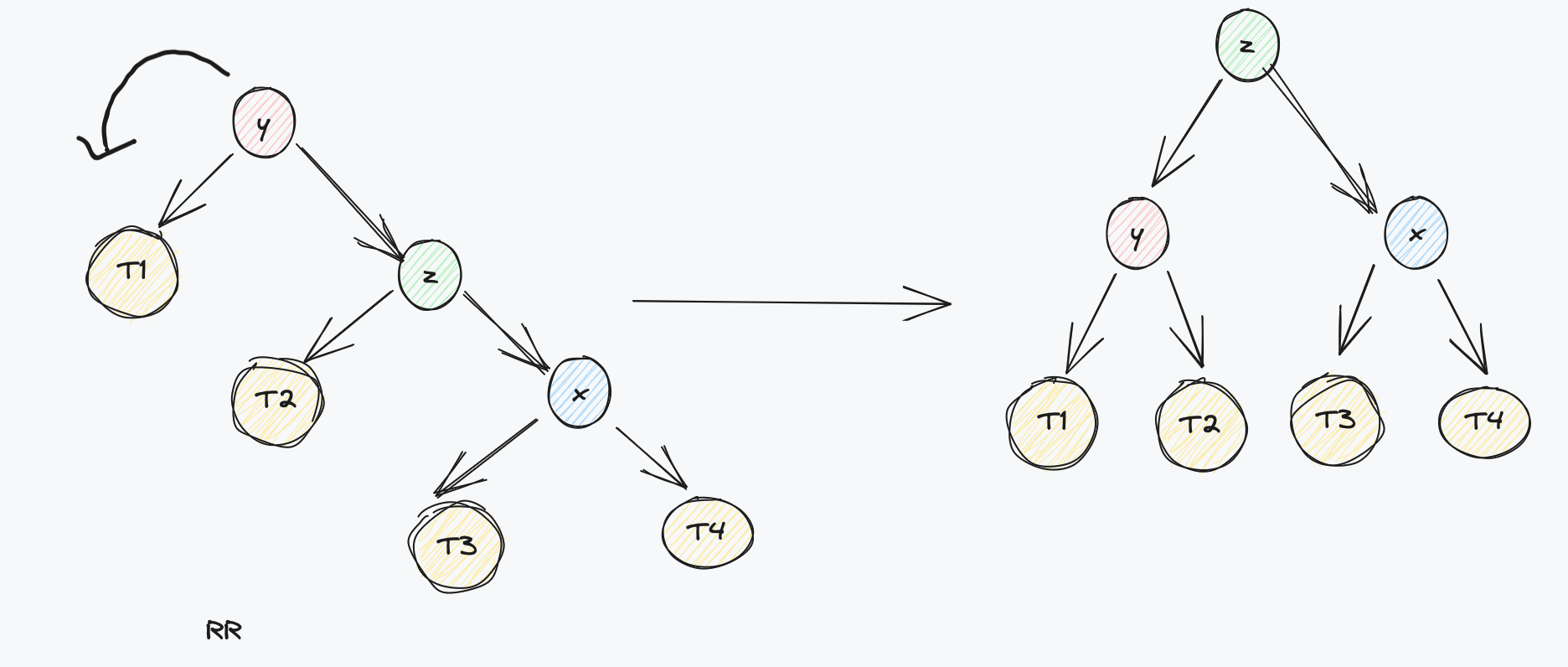
- RR 情况
根节点平衡因子小于-1,且左子树和右子树的高度差小于等于0
处理RR情况需要将树整体进行左旋转(即对根节点Y进行左旋转逆时针),效果如图所示:
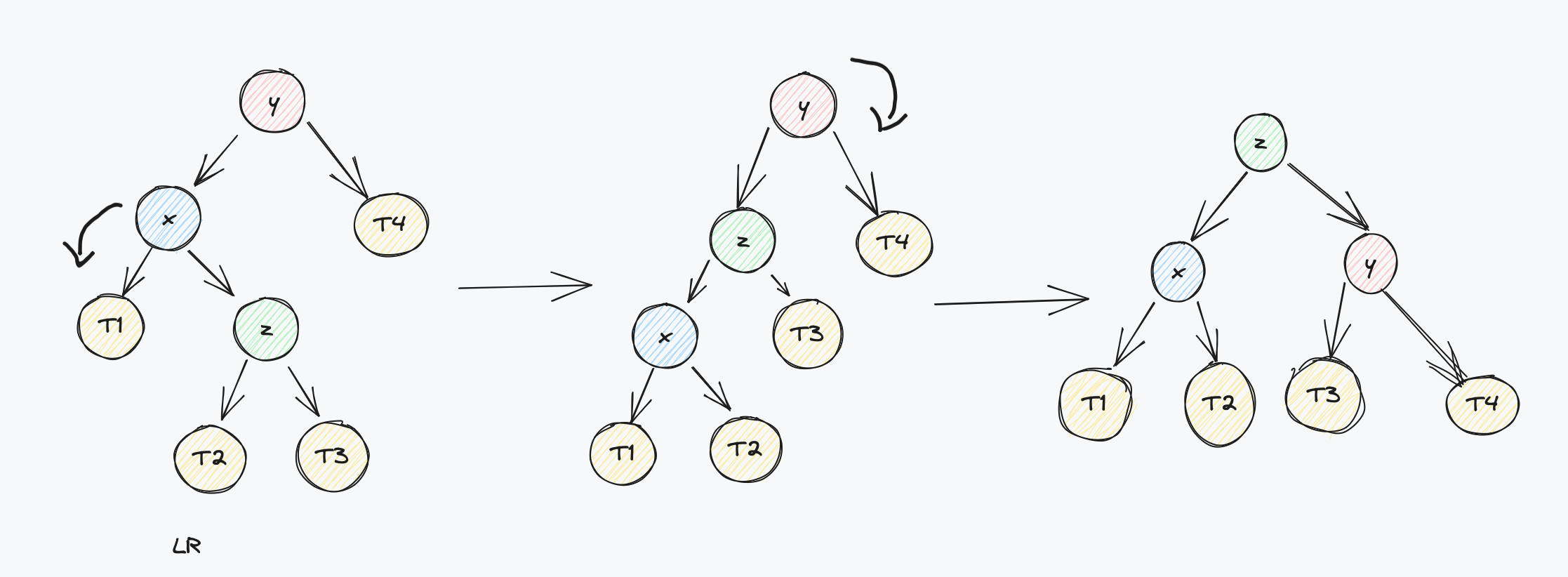
- LR 情况
根节点平衡因子大于1,且左子树和右子树的高度差小于0
处理LR情况需要将其左子树进行左旋转 为LL,然后在将整体树进行右旋转,效果如图所示:
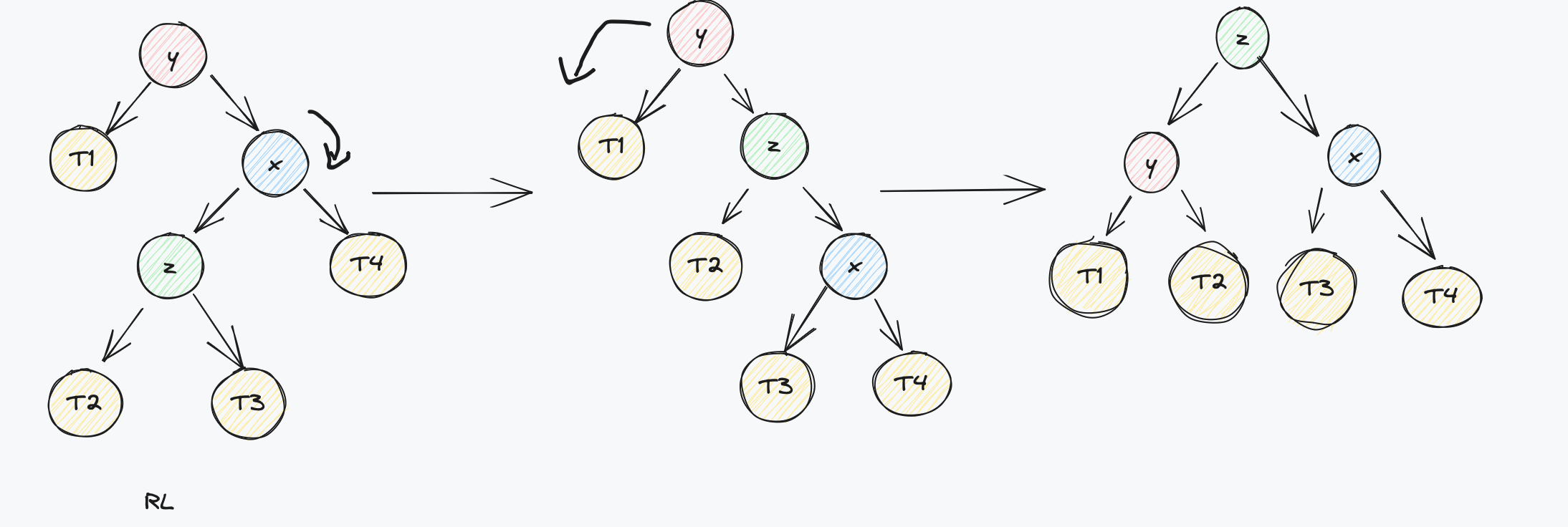
- RL 情况
根节点平衡因子小于-1,且左子树与右子树的高度差大于0
处理RL情况需要将其右子树进行右旋转 为RR,然后再将整体树进行左旋转,效果如图所示:
删除节点
从AVL树中删除,可以通过把要删除的节点向下旋转成一个叶子节点,接着直接移除这个叶子节点来完成。因为在旋转成葉子節點期间最多有log n个节点被旋转,而每次AVL旋转耗费固定的时间,所以删除处理在整体上耗费O(logN)